Si ![]() , on peut par plusieurs méthodes démontrer que
, on peut par plusieurs méthodes démontrer que ![]() . On va citer trois méthodes, parmis lesquelles il y’a une méthode qui prouve que généralement si
. On va citer trois méthodes, parmis lesquelles il y’a une méthode qui prouve que généralement si ![]() et
et ![]() alors
alors ![]() . On commence par la première méthode qui utilise un argument de densité, par suite elle a un inconvénient, c’est le fait qu’elle est valable pour le cas où le corps de base
. On commence par la première méthode qui utilise un argument de densité, par suite elle a un inconvénient, c’est le fait qu’elle est valable pour le cas où le corps de base ![]() est un sous-corps de
est un sous-corps de ![]() pour pouvoir utiliser la notion de norme nécessité par la topologie sur quoi on se base pour définir la densité.
pour pouvoir utiliser la notion de norme nécessité par la topologie sur quoi on se base pour définir la densité.
Première méthode: Densité de 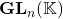
Dans tout ce qui suit ![]() est un sous-corps de
est un sous-corps de ![]() , on rappelle que
, on rappelle que ![]() est dense dans
est dense dans ![]() , si
, si ![]() et
et ![]() , alors,
, alors, ![]() . Les matrices
. Les matrices ![]() et
et ![]() sont donc semblables, donc
sont donc semblables, donc ![]() . Si
. Si ![]() , par densité, il existe une suite
, par densité, il existe une suite ![]() tel que
tel que ![]() . Pour tout
. Pour tout ![]() , on a:
, on a: ![]() et comme les applications
et comme les applications ![]() et
et ![]() sont continues, le passge à la limite permet d’avoir
sont continues, le passge à la limite permet d’avoir ![]() .
.
Deuxième méthode: Utilisation de la matrice 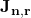
Préliminaire avant de commencer:
Avant de commencer remarquons que si ![]() tel que
tel que ![]() et
et ![]() avec
avec ![]() , alors
, alors ![]() et
et ![]() , de sorte que:
, de sorte que: ![]() et
et ![]() , donc
, donc ![]() .
.
Par ailleurs, comme on l’a démontré dans la première méthode notons que ![]() , pour toute matrice
, pour toute matrice ![]() et toute matrice inversible
et toute matrice inversible ![]() .
.
Preuve pour la deuxième méthode:
Si ![]() , alors si
, alors si ![]() alors
alors ![]() donc
donc ![]() et le résultat devient évident.
et le résultat devient évident.
Si ![]() , alors
, alors ![]() est inversible et alors
est inversible et alors ![]() et
et ![]() sont sembalbale et le résultat a lieu.
sont sembalbale et le résultat a lieu.
Finalement, si ![]() , il existe
, il existe ![]() tel que
tel que ![]() où
où ![]() . Donc , en notant
. Donc , en notant ![]() la matrice
la matrice ![]() et compte tenu , on a:
et compte tenu , on a: ![]()
est ce que cette demo est valable pour tout corp K
Celle de la deuxième méthode oui, mais celle qui utilise la densité il faut prendre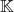 un sous corps de
un sous corps de 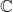
merci , monsieur