1 Réponses
Pour la troisième question on a généralement pour tout ![]() , la somme
, la somme ![]() , et comme
, et comme ![]() , si
, si ![]() est le reste de la division euclidienne de
est le reste de la division euclidienne de ![]() par
par ![]() , on a
, on a ![]() , donc
, donc 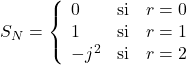 . En fait c’est
. En fait c’est ![]() dans le troisième cas mais
dans le troisième cas mais ![]() donne
donne ![]() . Dans le cas
. Dans le cas ![]() , on a
, on a ![]() , donc
, donc ![]() donc la somme demandée vaut:
donc la somme demandée vaut: ![]() .
.
Mohamed AL Commentaires modifiés

vu ce jour, je rappelle que le nombre complexe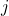 est
est 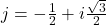 , et que son écriture exponentielle est
, et que son écriture exponentielle est 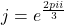 .
.