1 Réponses
On a ![]() , donc
, donc ![]() . Donc
. Donc ![]() , donc
, donc ![]() .
.
- Pour calculer
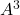 , on peut utiliser
, on peut utiliser 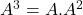 et les expressions respectives de
et les expressions respectives de 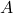 et
et 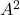 .
. - Pour calculer
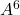 , on peut utiliser
, on peut utiliser 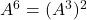 .
. - Finalement
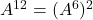 .
. - En utilisant le logiciel Maple, je trouve les résultats suivants(voir l’image ci-dessous pour une copie d’écran):
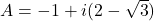 ,
,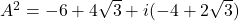 ,
,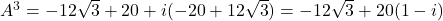 ,
,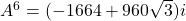 .
.- Bien entendu, ce n’est pas la peine de faire un calcul explicite de
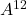 , il faut juste se contenter de dire que c’est le carré d’un imaginaire pur donc il est réel.
, il faut juste se contenter de dire que c’est le carré d’un imaginaire pur donc il est réel.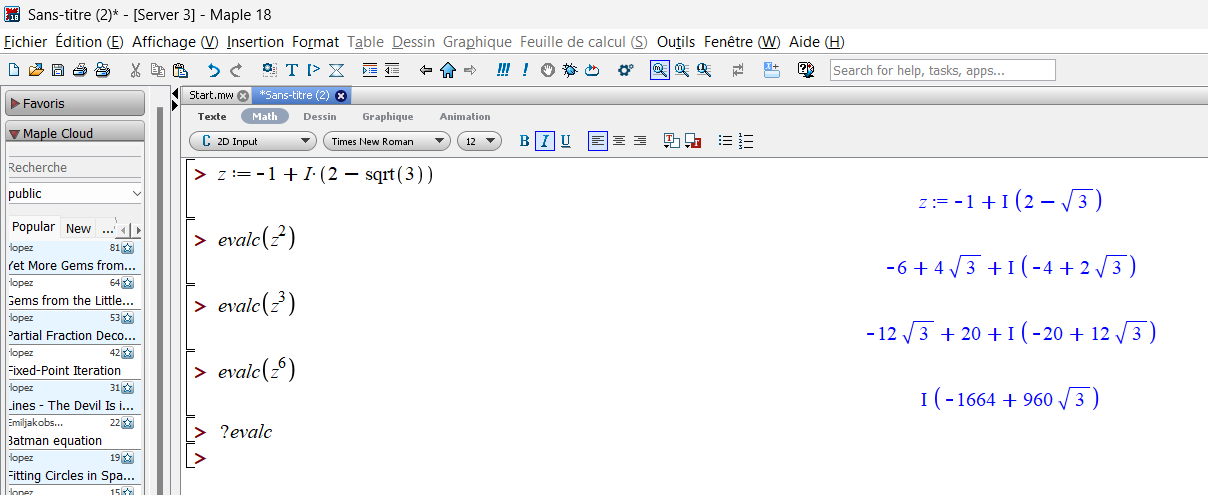
Mohamed AL Changer le statut à "publié"

Il y’a beaucoup de calculs mais c’est nécessaire pour une bonne évolution en mathématiques, les calculs apprenne beaucoup de chose et imposent une volonté de se concentrer.