On se propose de donner une idée pour démontrer que si ![]() est un espace vectoriel sur
est un espace vectoriel sur ![]() de dimension au moins
de dimension au moins ![]() et si
et si ![]() est un endomorphisme de
est un endomorphisme de ![]() alors
alors ![]() admet au moins un plan stable. En fait si
admet au moins un plan stable. En fait si ![]() est un corps quelconque et
est un corps quelconque et ![]() admet au moins une valeurs propre alors
admet au moins une valeurs propre alors ![]() admet au moins une droite stable, c’est le cas notamment si
admet au moins une droite stable, c’est le cas notamment si ![]() , mais si
, mais si ![]() n’admet aucune valeur propre une telle droite stable n’existe pas et pour
n’admet aucune valeur propre une telle droite stable n’existe pas et pour ![]() on a quand même un plan, donc en résumé si
on a quand même un plan, donc en résumé si ![]() est un
est un ![]() espace vectoriel non nul et
espace vectoriel non nul et ![]() ou
ou ![]() alors pour tout endomorphisme
alors pour tout endomorphisme ![]() de
de ![]() il existe au moins une droite ou un plan stable par
il existe au moins une droite ou un plan stable par ![]() .
.
Cas où 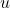 admet au moins une valeur propre:
admet au moins une valeur propre:
Si ![]() admet au moins une valeur propre(c’est le cas si
admet au moins une valeur propre(c’est le cas si ![]() ou
ou ![]() et
et ![]() est impair), alors si on note
est impair), alors si on note ![]() une telle valeur propre et
une telle valeur propre et ![]() un vecteur propre associé, la droite
un vecteur propre associé, la droite ![]() est stable par
est stable par ![]() car si
car si ![]() , il existe
, il existe ![]() tel que
tel que ![]() , donc
, donc ![]() , donc
, donc ![]() .
.
Cas où 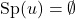 et
et 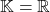 :
:
Si ![]() et
et ![]() , les facteurs irréductibles du polynôme caractéristique de
, les facteurs irréductibles du polynôme caractéristique de ![]() sont tous des trinômes
sont tous des trinômes ![]() unitaires de discriminants strictement négatifs. Donc
unitaires de discriminants strictement négatifs. Donc ![]() , et comme
, et comme ![]() , il existe
, il existe ![]() tel que
tel que ![]() est non injectif car si les
est non injectif car si les ![]() sont tous injectifs il en serait de même de leur produit, donc
sont tous injectifs il en serait de même de leur produit, donc ![]() serait injectif, ce qui n’est pas le cas car c’est l’endomorphisme nul. On peut donc dire qu’il existe
serait injectif, ce qui n’est pas le cas car c’est l’endomorphisme nul. On peut donc dire qu’il existe ![]() tel que
tel que ![]() est non injectif, donc il existe un vecteur non nul
est non injectif, donc il existe un vecteur non nul ![]() tel que
tel que ![]() , donc
, donc ![]() , donc si
, donc si ![]() alors
alors ![]() est un plan de
est un plan de ![]() stable par
stable par ![]() .
.